

「黄金律」は生命の創造に関する「律」です。円と同様の根本原理であり、三位一体に当てはめるなら「円」+「黄金律」=「生命」と表せる円の対になる理です。「最も古き者」「円」の力は無限ですが、いくら無限であろうと”それ”だけでは力は循環するばかりで形を成せません。最も古き者の力をこの世に顕現させるには「絶妙な律」が必要です。円のように永遠に繰り返し、かつ拡張・縮小が行える絶妙な律、それが黄金律です。
我々人間がその姿を認識するには二つの方法があります。一つは数、一つは図形です。黄金律が「知恵の女神」や「美の女神」として象徴化される理由として、その数と図形から知恵を通して真の美しさが理解できることが挙げられます。では知恵を使いながら黄金律に関する数と図形を順に見てゆきましょう。

まずは「円」の項の最初と同じく、この格言から始めます。「個は全 全は個」。正負の対をなす個が全となり、その全はまた新たな個となる「個+個=全」の繰り返し、いわゆる「三位一体」の理を表す格言です。この普遍の原理を単独で表すのは円ですが、数で正確に表すのは「1.618033..」の黄金律です。
黄金律はその数列自体に意味がある訳ではございません。黄金律が現れる時には必ず二つのモノが存在し、その関係に黄金律が現れます。つまり二つのモノの間に存在する「比」に黄金律が現れるということ。故に「黄金比」との名称が先行し広まっていますが、正確には「黄金律」であり、重ねて述べますがそれは二つのモノの比率に現れます。
「比」は古代ギリシア語で「ロゴス」と言います。宗教体系によっては唯一神を「ロゴス」と呼ぶほどの重要な知恵です。「比」とは、ある数が他の数の何倍にあたるかという関係を表しています。この比に関して古代の賢人プラトンは「長い方に対する全体の比が、短い方に対する長い方の比と等しくなる」そんな特別な比を見つけよと残しました。こんな不可思議な条件を満たす特別な比はこの世に一つしか存在しません。
そう、黄金比です。

さて知恵を使う時間です。プラトンの言葉は一見不可解ですが、数で見れば的を得た確かな言葉です。個は全体を表し、全体はまた個を表す。この言葉を念頭に上図のa,b,cに数を当てはめてゆきます。「aは長い方」「bは短い方」「cは全体」です。
長い方に対する全体の比が、短い方に対する長い方の比と等しくなる比
全体(c)が1.618の場合、長い方(a)が1で短い方(b)が0.618です。
-
長い方に対する全体の比 = 1.618 ÷ 1 = 1.618
-
短い方に対する長い方の比 = 1 ÷ 0.618 = 1.618
全体が1の場合、長い方が0.618で短い方が0.381です。
-
長い方に対する全体の比 = 1 ÷ 0.618 = 1.618
-
短い方に対する長い方の比 = 0.618033 ÷ 0.38192 = 1.618
全体が0.618の場合、長い方が0.38192で短い方が0.23602です。
-
長い方に対する全体の比 = 0.618 ÷ 0.38192 = 1.618
-
短い方に対する長い方の比 = 0.38192 ÷ 0.23602 = 1.618
こんな神がかった比率だからこそ「円の力」を絶妙なバランスで秩序立てられるのです。故に黄金律と定義されます。しかしながら少々数字の羅列が過ぎますね。これでは数字に慣れていない人では嫌になってしまいます。そこでもっとエレガントな表現になおしましょう。黄金比は「美」そのもの。ですから上記の数字の羅列も美しい記号に置き換えれば、より美しく見えます。その記号とは「Φ」。パルテノン神殿に黄金分割を用いたギリシアの建築家フィディアスの頭文字にちなみ「Φ」「ファイ」とされています。1.618が「Φ」「ファイ」、0.618が「φ」「フィー」です。では上記の数式を美しい記号に置き換えます。
全体がΦの場合、長い方が1で短い方がφです。
-
長い方に対する全体の比 = Φ ÷ 1 = Φ
-
短い方に対する長い方の比 = 1 ÷ φ = Φ
全体が1の場合、長い方がφで短い方がφ²です。
-
長い方に対する全体の比 = 1 ÷ φ = Φ
-
短い方に対する長い方の比 = φ ÷ φ² = Φ
全体がφの場合、長い方がφ²で短い方がφ³です。
-
長い方に対する全体の比 = φ ÷ φ² = Φ
-
短い方に対する長い方の比 = φ² ÷ φ³ = Φ
少々乱暴ですが簡潔に書けば、
φ³ に Φをかけると φ² になり、
φ² に Φをかけると φ になり、
φ にΦをかけると1になり、
1に Φをかけると Φ になり........
これがプラス方向にもマイナス方向にも延々と続きます。
ピタゴラス学派が大切にした三項連続比例式で表しますと、上記の関係は以下の式のようにとても美しくまとまります。
Φ:1::1:φ
もう一つ、Φの特性としまして「繰り返し」があります。お気づきかとは思いますが、小数点以下の「618」のことです。二乗して同じ数が現れる数字はΦだけです。
1.618 × 1.618 = 2.618
上記の性質を理解しますと以下の式が理解できます。唯一無二の式です。
-
X² − X − 1 = 0
-
Φ² − Φ − 1 = 0
-
1.618² − 1.618 − 1 = 0
以上のことから読み取れる理は生命の「成長」であり詳細に申し上げれば「自己相似」「自己複製」です。生命は突然大きくなったり小さくなったりはしません。少しづつ成長をしてゆきますが、その全体は成長のどの段階においても「全体とその他の部分」との比率で黄金比を保ちます。また、その形も急に突飛な形にはならず、必ず自己相似・自己複製を経て拡大・縮小します。アンモナイトの断面が分かりやすいのでwikiから引用します


周回しながら成長する貝を何周目で切ったとしても、「全体」と「全体を構成する渦」の比率は一定であり黄金比を保ちます。その形は貝の中心の渦の「自己相似」「自己複製」であり決して崩れません。そして、この構造は先にも述べましたが根本原理です。下がこうなら上もこうです。では上を見てみましょう。我々が住む太陽系が属する銀河の姿です。銀河に対して太陽系が周回している場所(赤矢印)にも注意してください。そのポイントは銀河の中心から淵までの直線を黄金比率で分割するポイントです。

これまでで、黄金律が二つのモノの比に現れること、その比とはΦとφであり「成長」「自己相似」の根本原理を体現していること、この2点について述べてまいりました。円の項とこれまでに本項で述べた基本的な事をまとめますと、円の無限の力は黄金律の美しさがなければ顕現できず、また逆に黄金律の美しさも円の力がなければ顕現できません。
「円の力と美しい比」
この対で宇宙の中心から淵まで全てが整っています。つまりこの宇宙に存在するもの全てが従う秩序です。故に宇宙のどこを切り取っても必ずその証が現れます。ではここから黄金律がどのように自然に関わっているのかに焦点をあて進めてゆきます。
黄金律は「孤高の円」とは違いその姿は多種多様です。二つのモノの間の比率に現れますので、それが「比」だったり「数」だったり「角度」だったりします。比というのはこれまでに述べてきた「黄金比」、数というのは「フィボナッチ数列」、角度というのは「葉序」の事です。どれからもはっきりと黄金律が現れます。
動画内で登場しました「フィボナッチ数列」は自然界の至る所で目にする黄金律の現れです。この数列は0から始まり、0.1.1.2.3.5.8.13.21.34.55.89.144..... となる数列で、どの数も先行する二つの数の和です。そして、隣り合う数同士の比率は全てΦの近似であり桁数が増えれば増えるほどΦに近づきます。
-
1/1=1
-
2/1=2
-
3/2=1.5
-
5/3=1.6666
-
8/5=1.6
-
13/8=1.625
-
21/13=1.6154
フィボナッチ数列と黄金比の関係を理解できれば「黄金螺旋」の仕組みも理解できます。

画像の螺旋は全て正方形の対角を繋ぐ弧の繰り返しです。その正方形の1辺の長さはフィボナッチ数で増えてゆきます。ですから円の1/4づつ広がり螺旋を形成する弧は、1/4づつ黄金比で拡張してゆきます。故に「黄金螺旋」なのです。円の無限の力と黄金律が結びついたその姿は、ただ繰り返す円環ではなく無限に拡張・縮小する螺旋です。
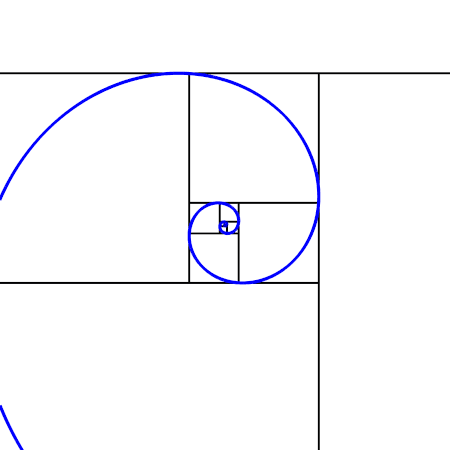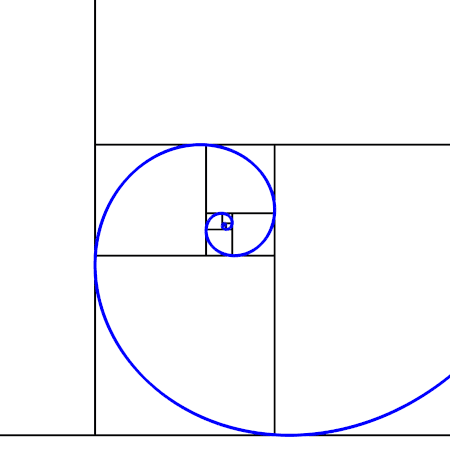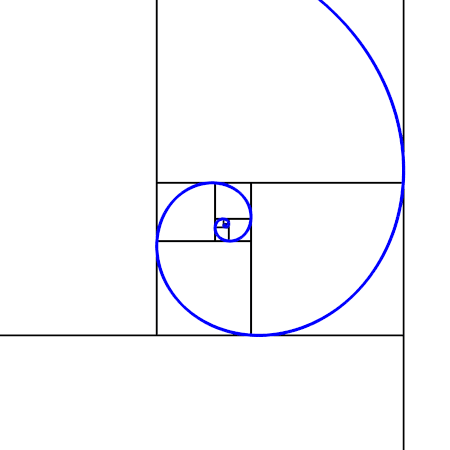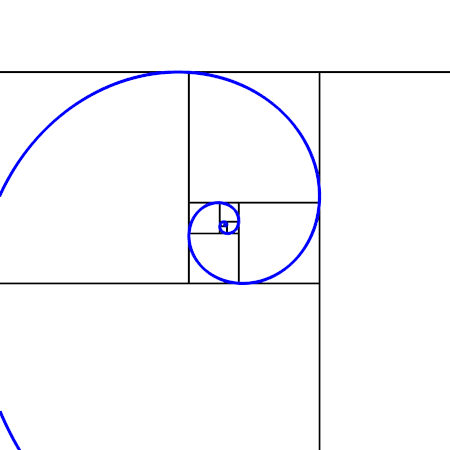
余談ですが、フィボナッチ数にも円と同じように面白い繰り返しが隠れています。円周率の360番目から前3つの数が360だったように(円の角度は360°)、フィボナッチ数にも隠れているのです。フィボナッチ数の12番目の数「89」で「1」を割ると、、、、
1 ÷ 89 = 0.011235......
フィボナッチ数列の最初の「6」桁が現れます。フィボナッチ数からフィボナッチ数が現れるのです。その総和は「12」でまたまた繰り返します。0 + 1 + 1 + 2 + 3 + 5 = 12
フィボナッチ数列の仕組みが理解できれば、その兄弟のような数列も理解できます。それは「リュカ数」と呼ばれる数列です。仕組みはフィボナッチ数列と同じで、どの数も先行する二つの数の和であり隣り合う数の比は黄金比ですが「始まりの数」だけ違います。フィボナッチ数列はゼロから始まりますがリュカ数は「2」から始まります。
2 . 1 . 3 . 4 . 7 . 11 . 18 . 29 . 47 . 76 . 123 . 199.....
リュカ数からは正負の拮抗状態が驚くようなバランスで読み取ることができます。リュカ数列を作る整数は絶妙な正負のバランスの上に成り立つ整数なのです。しかも、その式はプラスとマイナスが順に入れ替わりながら進みます。百聞は一見に如かず。数式を見てみましょう。
-
「2」= Φ + φ² 1.61803398 + 0.38196601
-
「1」= Φ − φ 1.61803398 − 0.61803398
-
「3」= Φ² + φ² 2.61803398 + 0.38196601
-
「4」= Φ³ − φ³ 4.23606797 − 0.23606797
-
「7」= Φ⁴ + φ⁴ 6.85410196 + 0.14589803
-
「11」= Φ⁵ − φ⁵ 11.09016994 − 0.09016994
さて、ここでテスラの残した3.6.9の秘密の意味を思い出してください。1から9までの数で理を伝えるロディンフラクタルです。この意味は掛け算から読み取れます。
では掛け算とロディンフラクタルを踏まえまして、上記リュカ数の数式の「+部分」の式をみてみましょう。桁数が多いので「掛け算」の動画のように分かり易いよう上下に配置します。ですがいくら桁数が多いと言っても簡単に暗算できますでしょ?答えは一つなのだから。
1.61803398
+ 0.38196601
1.99999999
2.61803398
+ 0.38196601
2.99999999
6.85410196
+ 0.14589803
6.99999999
+部分の式の和の小数点以下は全て9になります。またマイナス部分の式を構成する数の小数点以下は全く同じ数です。
人間の巧妙さが、自然が創造するものよりも美しくシンプルな、あるいは正確な発明をすることは決してできない。なぜなら自然の女神の創造物には何一つ欠けるところがなく、何一つ過分なものがないからである
レオナルド・ダ・ヴィンチ
あらゆるものの部分はそれ自身のうちに全体の性質を保っている
レオナルド・ダ・ヴィンチ
あらゆるものは他のあらゆるものと繋がっている
レオナルド・ダ・ヴィンチ
ダヴィンチ先生の格言三連発です。いかがでしょう?以前より先生の言葉が理解できますでしょうか?何を伝えたいのか、何を説明しているのかご理解いただけましたか?ではもう一発先生の言葉をぶっ込みましてフィボナッチ数列とリュカ数列をまとめます。
理解するための最良の手段は自然の無限の作品を十分に鑑賞することである
レオナルド・ダ・ヴィンチ

葉から次の葉までの角度を「葉序」と言います。その角度は成長の度合いによっていくつか存在しますが最終的には137.5°に近づいてゆきます。この137.5°の数式は
360 ÷ Φ² = 137.5
成長の度合いによって変わる葉序は全てフィボナッチ数列(赤字)由来です。
双葉 = 180° = 2/1
三つ葉 = 120° = 3/1
五つ葉 = 144° 〜 216° = 5/2 〜 5/3
八つ葉 = 135° 〜 225° = 8/3 〜 8/5
観察された全ての植物の開度のおよそ92%が「フィボナッチ数列」由来です。また、たった1.5%ですが「リュカ数列」由来です。

木の枝の分岐はフィボナッチ数列です。幹の太さと枝の数の関係も面白いですね。

逆さまにしますと人間の肺になります。そりゃそーですわよ、植物も人間も同じ自然の一部なのだから。あっ、可愛い動物も同じ仲間であることをお忘れなく。

この世に存在するもの全てが自然の一部であり仲間です。人間が上で動物が下なんてこともありません。人間も動物も植物も全て同じ仲間です。円や黄金率の根本原理を学ぶことにより、仲間の証がはっきりと認識でき、偽善的な建前の「皆仲間」ではなく、
心の底から全ては繋がっているのだと理解できたはずです
その時に湧き上がる感情が喜びです。真の喜びです。自然を学び理解することでしか到達できない喜びです。では本項「黄金律」の締めとしまして、しつこいですがダヴィンチ先生のお言葉を引用します。
最も高貴な娯楽とは理解する喜びである
レオナルド・ダ・ヴィンチ
関連記事:「花と星」
黄金律の塊の図形である「五芒星」に関しましては過去記事で何度も取り上げておりますので上記の関連記事、またはYoutube「Flower & Planet 花と星」をご覧くださいまし。


